之前介绍了插入操作，简单总结就是如果平衡出现问题，先向上递归染色成父红叔黑状态，然后根据LL/RR/LR/RL进行右旋(针对g节点)/左旋(针对g节点)/左旋(针对p节点)+右旋(针对g节点)/右旋(针对p节点)+左旋(针对g节点)，最后互换颜色。
可以发现对于插入操作，我们可以一句话描述清楚所有场景，而对于删除操作，就比较复杂了。本文介绍删除操作的原理

删除操作

对于红黑树的删除操作，其全部操作分为两个阶段。

• 删除阶段：找到前驱/后继节点替换待删除节点
• 修复阶段：修复，平衡破坏，修复平衡

这两步操作宏观看还是非常好理解的，现在逐一介绍

删除阶段

对于删除阶段，主要有三种场景，我们先准备一下必要条件

1. 如果被删除节点没有子节点，那么其就相当于有两个空黑节点 (一种情况)
2. 如果被删除节点只有一个节点，那么被删除节点一定是黑色，被删除节点的子节点一定是红色 (两种情况)

因为被删除节点只有一个节点，而黑高必须平衡，所以子节点肯定得红色，又因为子节点必须是红色，所以被删除节点一定是黑色

3. 如果被删除节点有两个节点，理论上按照有2的3次方共计8种组合方式，但是根据红黑树的规定，不能连续的红色，则只有按照前序遍历的 黑红红/红黑黑/黑红黑/黑黑红 (四种情况) 好了，根据上面的必要条件，一共七种情况，我们可以直接开始逐个根据所有场景分析了。
   本文将相关节点如下称呼

• 待删除节点(s)
• 待替换节点(r)
• 父节点(p)
• 兄弟节点(b)
• 侄子节点(n)：兄弟节点的左/右孩子

没有子节点

这种情况下，就相当于有两个空节点，没有人替换它，我们不需要进行第一阶段删除，直接跳转到第二阶段修复去调整平衡

只有一个子节点

这里两种情况，子节点无论是左边还是右边，处理方式都是

• 删除节点s，把其孩子节点作为节点r替换为节点s
• 将节点s从红色染色成黑色

因为只有一个子节点的时候，由红色节点替代了被删除的黑色节点，此时修复黑高的方法就是将替代节点r的红色染成黑色即可。
故仅需两步，调整结束

有两个子节点

这种情况对应了其他四种场景，此时我们需要找到前驱节点或后继节点。也就是找到小于此节点的值或者大于此节点的值。所以关键点在于如何找到前驱节点和后继节点作为替代节点r。
而找前驱节点和后继节点的情况分别又是两种。

所以在 黑红红/红黑黑/黑红黑/黑黑红 四种场景下，我们根据红黑树的找前驱还是后继的方式可以两种实现(前驱/后继)来找节点r，在不同的实现下如何找前驱和后继还有两种方式，下面逐一介绍。

前驱方式

先介绍前驱方式寻找小于节点s的节点r

节点s的左子树没有右孩子

如果节点s的左子树没有右孩子，那么节点s的左孩子就是替代节点r，因为此时的节点r就是节点s的前驱节点。那么步骤如下：

1. 我们将节点r(前驱节点)替换到节点s上
2. 将节点r的颜色设置为节点s的颜色
3. 然后将节点r的左孩子强制设置为黑色

我们需要注意的是，节点r的左孩子只能是红色。原因如下：

如果节点r的左孩子是黑色，那么又因为节点r是单节点，黑高肯定不平衡，图示如下。

首先我们假设一个红黑树如下：

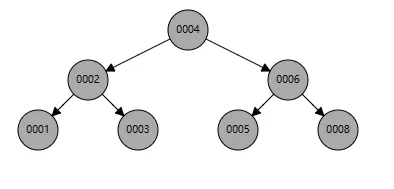
此时我们删除节点3，让其处于如下状态

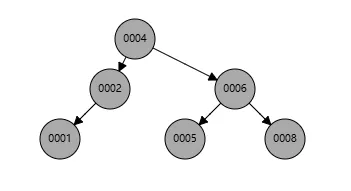
此时节点2相当于节点r，节点1相当于节点r的左孩子
我们算上叶子节点来计算黑高，可以发现，4-2 这里黑高是3，而其他的黑高是4。所以黑高一定不平衡。

那么我们可以得出结论，此情况下，节点r的左孩子一定是红色

根据上面的结论而言，我们的步骤相当于删除前驱节点r的颜色，然后再将节点r的左孩子强制设置为黑色。因为节点r的左孩子一定是红色，我们将节点r的左孩子强制染黑，黑高自然就是平衡了。

再补充一点，我们知道节点r的左孩子一定是红色，根据红色不能连续的规则，那么节点r一定就是黑色，在这种情况下，删除节点r的颜色就是删除了一个黑色，而为了维持黑高，将节点r的孩子染色成黑色，自然就平衡了。

节点s的左子树有右孩子

因为节点s的左子树有右孩子，我们就需要遍历其所有的右孩子，找到节点s的前驱节点。
值得注意的是，此时节点s的前驱节点r和节点s就没有相关性了。如我们步骤如下

1. 遍历其所有的右孩子，找到节点s的前驱节点

2. 我们将节点r(前驱节点)替换到节点s上

3. 将节点r的颜色设置为节点s的颜色

4. 然后将节点r的左孩子强制设置为黑色

上面三个步骤和节点s的左子树无右孩子的场景一致，但是我们在第三步将节点r的左孩子强制染黑了，而此时节点r和节点s没有相关性。所以黑高平衡破坏了之后，没办法直接修复，需要进行修复第二步骤。也就是如下

补充一下为什么没办法直接修复，因为节点s和节点r相差距离可能很远，我们是删掉了节点r，将节点r的内容放在节点s，实际上是因为节点r的丢失，导致从节点s的左边全部失去平衡。所以才有了第二步骤：修复

5. 将关注节点变成节点r的左孩子，进行第二步骤修复

后继方式

后继方式和前驱方式逻辑一致，操作方式是镜像的

节点s的右子树没有左孩子

步骤如下：

1. 我们将节点r(后继节点)替换到节点s上
2. 将节点r的颜色设置为节点s的颜色
3. 然后将节点r的右孩子强制设置为黑色

节点s的右子树有左孩子

我们需要遍历其所有的左孩子，找到节点s的前驱节点。
指的注意的是，此时节点s的前驱节点r和节点s就没有相关性了。如我们步骤如下

1. 遍历其所有的左孩子，找到节点s的后继节点

2. 我们将节点r(后继节点)替换到节点s上

3. 将节点r的颜色设置为节点s的颜色

4. 然后将节点r的右孩子强制设置为黑色

5. 将关注节点变成节点r的右孩子，进行第二步骤修复

总结

至此，我们针对最后四种场景下，根据找前驱和后继的方式，将原节点进行了删除操作，如果前驱/后继节点和节点s没有相关性，则我们需要开展第二阶段修复操作，否则我们强制染色就能维持平衡。接下来开始介绍红黑树删除的第二阶段：修复操作

修复阶段

在删除阶段，实际上我们目的是先将目标节点s删除，然后通过找前驱/后继的方式找到替代节点r，将其替换目标节点s。(其本质是删除了节点r)
而在修复阶段，实际上我们就需要将无法修复的黑高来进行进一步修复。

在这里，我们将兄弟节点称之为节点b，将侄子节点称之为节点n(ln/rn)，将关注节点称之为节点s，记得关注节点注意和第一阶段区分。

在修复阶段，一共五种情况， 如下：

1. 兄弟节点b是红色
2. 兄弟节点b是黑色，且节点b的左右孩子(节点ln和rn)都是黑色(包含空节点)
3. 兄弟节点b是黑色，且节点b的左孩子(节点ln)是红色，右孩子(节点rn)是黑色
4. 兄弟节点b是黑色，且节点b的左孩子(节点ln)是黑色，右孩子(节点rn)是红色

这里还有一种情况：

5. 兄弟节点b是黑色，且节点b的左右孩子(节点ln和rn)都是红色 这种情况和情况4合并

在上面五种情况下，我们还需要考虑关注节点s自身作为左孩子还是右孩子，这两种情况下，操作是镜像的。 为了方便介绍，我们先假设节点s自身作为父节点的左孩子。然后再介绍节点s自身作为父节点的右孩子的情况。

节点s是左孩子

假设节点s自身作为父节点的左孩子

兄弟节点b是红色

我们还是和插入的思想一致，如果兄弟节点b是红色的，我们要想办法让其变成黑色。

根据插入的时候的逻辑，假设是LL状态，那么我们对祖父节点右旋。这样自身插入节点向上一级。
同样的，如果是删除的时候，如果兄弟节点b是红色的，在L状态，为了让关注节点s向下降级，我们选择左旋。对谁左旋呢，当然是对父节点的左旋才能让关注节点s下降一级。

当左旋完成之后，节点s自降一级，我们知道节点b是红色的，那么节点b的任何子节点都一定是黑色的。那么左旋完成之后，兄弟节点肯定是黑色的。

这样我们就可以只讨论兄弟节点是黑色的情况了。

关于互换颜色，我们知道在插入操作后，会将兄弟节点b和父节点p颜色互换，同样删除也是。

对于左旋之后，我们需要的是将关注节点s的父节点p和祖父节点g的颜色互换

如果细心的可以了解到，对于颜色互换操作，其和插入操作是镜像的。 我列出如下

• 对于插入操作，LL状态下，右旋后将兄弟节点和父节点的颜色互换
• 对于删除操作，LL状态(左旋之后是LL状态)，左旋后将父节点和祖父节点颜色互换

也就是说，如果兄弟节点b是红色，那么再左旋完成之后，需要做一下颜色互换即可。互换的角色是

旋转后的 父节点和祖父节点。

总结一下，那么其步骤如下：

1. 将父节点p左旋
2. 将父节点p和祖父节点g交换颜色
3. 继续检查关注节点(因为左旋会让关注节点降级，所以可以继续关注节点)

至此，我们分析了情况1，它的目的是将兄弟节点染黑，染黑的操作是通过左旋完成(因为兄弟节点的子节点一定是黑色)，自身下降一级。

兄弟节点b是黑色，节点b的子节点都是黑色(包含空节点)

我们知道进入修复阶段的时候，红黑树已经不平衡了，那么如果兄弟节点b是黑色，且其子节点都是黑色，那么我们计算其兄弟的黑高一定是2，而关注节点和子节点的黑高是1或2(自身是红则是1,自身是黑则是2)。所以
我们可以发现，在这个状态，就是黑高不平衡的状态。

我们找到了不平衡的关键点。我们的操作是强制让其染红，也就是

强制给兄弟节点染红

当兄弟节点染红之后，我们得到的结果是兄弟的黑高固定为1，往上递归，找到所有兄弟节点b是黑色且所有侄子节点(ln/rn)是黑色节点的情况，把兄弟节点染红，让其黑高固定为1.(兄弟节点红色,两个侄子节点都是黑色)

此时，我们将兄弟节点强制染红了，那么对父节点p，就需要强制染黑，否则出现了连续的红色节点

总结一下，那么本情况下，其步骤如下：

1. 将兄弟节点b染色成红色
2. 将父节点p染色成黑色
3. 设置关注节点是父节点
4. 向上递归

兄弟节点b是黑色，左侄子是红色，右侄子是黑色

我们现在剩下三种情况，如下

1. 节点b是黑色，节点ln是红色，节点rn是黑色
2. 节点b是黑色，节点ln是黑色，节点rn是红色
3. 节点b是黑色，节点ln和rn都是红色

为了能够归一化这个问题，我们聚焦在一个点上：

• 右侄子节点(rn是红色)

为了让节点rn是红色，我们需要对 本情况1:节点b是黑色，节点ln是红色，节点rn是黑色 进行调整，调整步骤如下：

1. 兄弟节点b右旋
2. 交换兄弟节点b和节点ln的颜色

这样之后，我们发现，上述剩下的三种情况就变成两种情况了，我们继续情况4和5

兄弟节点b是黑色，左侄子是黑色，右侄子是红色

对于此情况，考虑到我们是删除操作，我们找到替代节点是前驱节点，前驱节点是找到左孩子的最右节点，实际上对于关注节点s，其黑高是少于右边的(因为删除过节点)，为了修复黑高，此时应该做的是左旋

因为左旋会将左侄子节点rn给关注节点作为关注节点的右节点

故步骤如下

1. 先左旋父节点p
2. 将祖父节点g的颜色设置为父节点p的颜色
3. 将父节点p的颜色设置为黑色
4. 将叔叔节点u的颜色设置为黑色

此时调整结束

兄弟节点b是黑色，左右侄子都是红色

其实根据插入的定义，我们插入时必须要保证父红叔黑，所以插入节点后，不会出现非底层节点出现两个红色

那么出现左右侄子都是红色的情况是 左右侄子节点ln/rn都只含有空节点

此时，我们的行为可以和情况4合并，因为最后将 左侄子节点rn给关注节点作为关注节点的右节点 的时候，这个右节点是红色的，它本身就维持平衡了，调整结束。

节点s是右孩子

这种情况和节点s是左孩子的情况是镜像的，主要如下

兄弟节点b是红色

那么此时的步骤如下：

1. 将父节点p右旋
2. 将父节点p和祖父节点g交换颜色
3. 继续检查关注节点(因为左旋会让关注节点降级，所以继续关注节点来修复)

兄弟节点b是黑色，节点b的子节点都是黑色(包含空节点)

那么此时的步骤如下

1. 将兄弟节点b染色成红色
2. 将父节点p染色成黑色
3. 设置关注节点是父节点
4. 向上递归

兄弟节点b是黑色，左侄子是黑色，右侄子是红色

那么此时的步骤如下

1. 兄弟节点b左旋
2. 交换兄弟节点b和节点ln的颜色

兄弟节点b是黑色，左侄子是红色，右侄子是黑色

那么此时的步骤如下

1. 先右旋父节点p
2. 将祖父节点g的颜色设置为父节点p的颜色
3. 将父节点p的颜色设置为黑色
4. 将叔叔节点u的颜色设置为黑色

兄弟节点b是黑色，左右侄子都是红色

此情况和 兄弟节点b是黑色，左侄子是红色，右侄子是黑色 情况一致，步骤也是一致

总结

红黑树的删除操作比较复杂，捋清楚需要认真思考很久，作为总结，删除操作简单来说如下，以节点s为左孩子为例：

1. 先进行删除操作
2. 删除操作中要找到替换节点，替换节点可能是左右子树，也可能是前驱节点，不同的红黑树实现，也可能使用后继节点实现
3. 当平衡产生破坏的情况下，需要进行修复操作
4. 修复操作的场景有五种，需要归一化处理
5. 先让兄弟节点变黑，向下继续
6. 如果兄弟节点和其子节点的黑高是2(都是黑的)，强行染色兄弟节点，让其黑高暂时是1
7. 根据5和6的操作，兄弟节点肯定是黑色，黑高不会一定是2
8. 此时想办法固定右侄子节点为红色
9. 如果右侄子为黑色，则对兄弟节点右旋，并交换颜色，此时右侄子一定为红色(因为原左侄子的红色给了右侄子)
10. 此时所有情况都归一化到：兄弟节点是黑，右侄子是红的情况
11. 将父节点左旋，完成后，强行将祖父节点设置为父节点颜色，并强行将父节点和叔叔节点染黑
12. 调整结束

在节点为右孩子时，我们左旋右旋的操作镜像即可。

本文将删除的原理彻底弄清楚了，为了方便理解，下一篇文章将所有的场景示例出来，加深印象。