你开心就好
rb-tree实现-基本要素
编辑
2025-04-07
记录知识
0
请注意，本文编写于 81 天前，最后修改于 59 天前，其中某些信息可能已经过时。

目录

树的结构
红黑树结构
红黑树特性
红黑树基本操作
左旋
右旋
总结

操作系统在实现调度的时候会使用rb-tree，可见红黑树对于操作系统而言是多么的重要，本文首先介绍一下rb-tree的基本要素，后面连载逐渐了解rb-tree

树的结构

对于一个树的结构，默认的实现应该如下

struct Node {
	struct Node *left;		/* left element */
	struct Node *right;		/* right element */
}

这里通过Node就是树的节点，left是树的左子树，right是树的右子树

此时我们新增一个parent的Node指针，这样我们可以查找树里面的元素就无需每次从根节点遍历，结构体如下

struct Node {
	struct Node *left;		/* left element */
	struct Node *right;		/* right element */
	struct Node *parent;		/* parent element */
}

红黑树结构

对于红黑树，我们需要对Node添加颜色标识，可以如下

struct Node {
	struct Node *left;		/* left element */
	struct Node *right;		/* right element */
	struct Node *parent;	        /* parent element */
	int rbe_color;			/* node color */
}

这样，我们基本的红黑树的数据结构就完成了，接下来说明红黑树的特性

红黑树特性

对于红黑树的基本特性，主要是如下四点

  • 根节点是黑色的
  • 叶子节点都是黑色的，这里叶子节点包括最后一个null的节点（左右均null）
  • 相邻的节点之间不能出现连续的红色
  • 从根节点到叶子节点的黑色节点数目相等

这里以 Data Structure Visualizations 网站绘图

https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

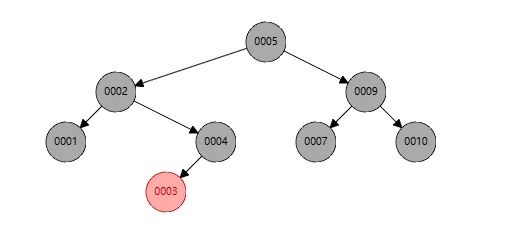
下面展示一个从1-10共10个元素的红黑树图

image.png

可以发现：

  • 对于特性1，节点6是黑色的
  • 对于特性2，图中我故意未画出
  • 对于特性3，节点1，3，9并不连续
  • 对于特性4，节点6，4，2和6，4，5和6，8，7和6，8，10的黑色节点数目相等

红黑树基本操作

红黑树的操作主要是左旋和右旋，以及插入和删除和搜索和染色，本文仅讨论左旋和右旋基本操作，插入，删除，搜索，染色等操作后面文章详细介绍。

关于左旋和右旋操作，是在红黑树出现不平衡的情况下，主动通过左旋和右旋调整使得整个红黑树平衡

左旋

对于左旋，就是红黑树不平衡的时候，对不平衡的节点向左旋转
假设有节点 x，y，a，b，r， 对其进行围绕x的左旋，如下所示

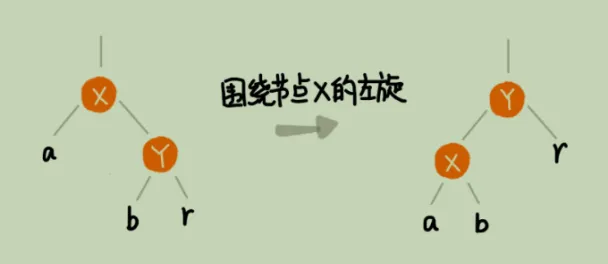
image.png

那么其具体步骤如下

  • 将节点x的right断开
  • 设置x的right节点y作为自己的parent
  • 如果节点y有left节点，则将y的left设置为x的right

简单理解就是，基于谁的节点左旋，就是将那个节点的右节点作为自己的父节点，然后重建叶子节点

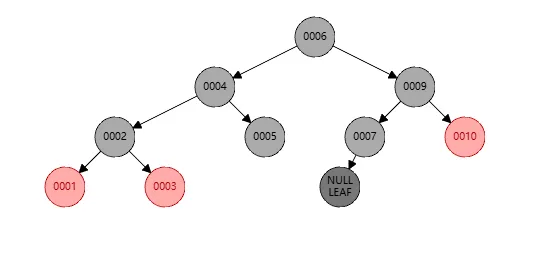
为了更清楚的了解左旋步骤，我基于最上面10个元素的示例演示，先删除了节点8，则此时的树结构如下

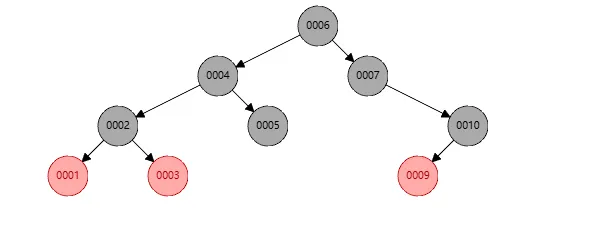
image.png

此时因为节点7没有左孩子，但是节点10有左孩子，这并不平衡，所以需要对节点10进行右旋，右旋我们还没解释，简单理解就是将自己的左孩子作为自己的父亲。所以右旋后结构如下

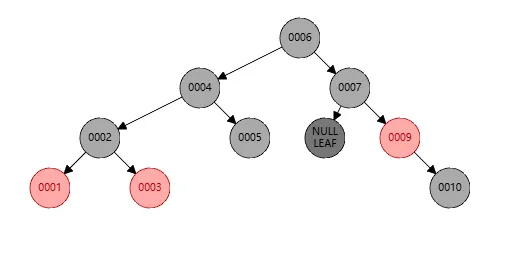
0003a0705c258bbc994c8c5ade228be.png

我们发现节点9不平衡，其左孩子的黑色个数是3，而其他个数是4，所以将其染色如下

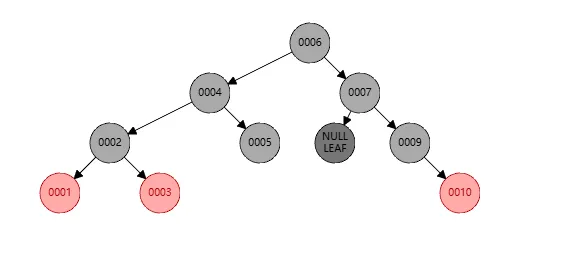
image.png

现在重点来了，但是此时节点7的左孩子是空，也就是其黑色节点数是3，我们需要左旋，步骤如下：

  1. 此时左旋的操作是针对节点7
  2. 对于7，断开节点9的连接，让其成为7的父节点
  3. 然后让节点7成为节点9的左孩子
  4. 因为节点9没有左孩子，所以无需进一步操作

这样左旋完成之后，结果如下

34d97652a4d4deb029511c5fce407b3.png

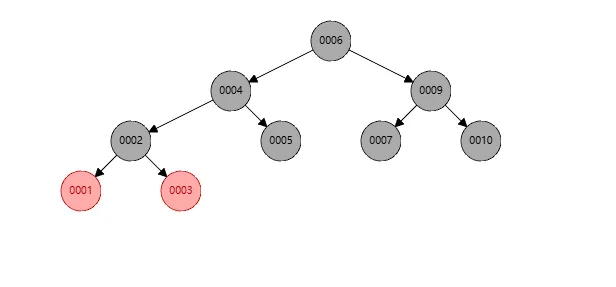
此时还是黑色个数不对，我们将节点10染色成黑色即可。如下

01ee401dbf545346968218c0ea4a8c4.png

右旋

我们介绍了左旋，对于右旋，就是红黑树不平衡的时候，对不平衡的节点向右旋转
假设有节点 x，y，a，b，r， 对齐进行围绕x的右旋，如下所示

image.png

那么其具体步骤如下

  • 将节点x的left断开
  • 设置x的left节点y作为自己的parent
  • 如果节点y有right节点，则将y的right设置为x的left

简单理解就是，基于谁的节点右旋，就是将那个节点的左节点作为自己的父节点，然后重建叶子节点

还是为了示例，还是基于上图删掉节点8之后的红黑树，此时我删除节点6，这里节点5会取代节点6，如下

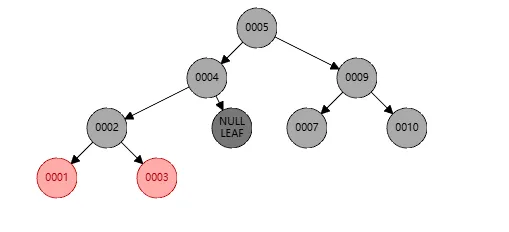
image.png

此时红黑树在节点4上不平衡了，我们需要针对节点4进行右旋
步骤如下：

  1. 此时左旋的操作是针对节点4
  2. 对于4，断开节点2的连接，让其成为4的父节点
  3. 然后让节点4成为节点2的右孩子
  4. 因为节点2有右孩子，所以将节点2的右孩子给节点4作为节点4的左孩子

这样右旋完成之后，结果如下

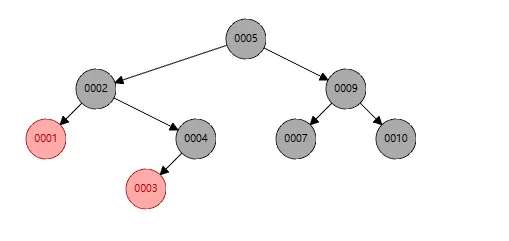
image.png

最后发现节点2的黑色节点不平衡，个数不对，所以将节点1染色成黑色即可完成，如下

image.png

总结

本文作为红黑树介绍的开头，简单介绍了红黑树的基础，例如红黑树的特性，红黑树的左旋和右旋操作。